1.堆定义
堆是一种数据结构,它是完全二叉树, 也可以称为二叉堆。
堆分为最大堆和最小堆
- 最大堆:任意节点的值不大于其父亲节点的值。
- 最小堆:任意节点的值不小于其父亲节点的值。
2.堆有什么用途
堆最常用于优先队列以及相关动态问题
优先队列指的是元素入队和出队的顺序与时间无关,既不是先进先出,而是根据元素的重要性决定。
3.堆的物理存储
堆的存储方式不是链式存储,而是顺序存储。二叉树所在的节点都在数组当中。
利用数组下标作为节点编号,假设父节点的下标是parent。则有
- 左儿子的下标 = 2* parent +1
- 右儿子的下标 = 2*parent +2
4.堆的操作
- 插入节点push
- 删除节点pop
这两种操作都是基于对的自我调整完成的
5.堆的自我调整
以最小堆为例
5.1 插入节点
二叉堆的节点插入,插入位置是完全二叉树的最后一个位置。比如我们插入一个新节点,值是0
这时候,我们让节点0与他的父节点5进行比较,0小于5,则新节点上浮,和父节点交换位置。
继续用节点0和父节点3作比较,如果0小于3,则继续交换
继续比较,最终让新节点0上浮到了堆顶位置。
5.2 删除节点
二叉堆的节点删除过程和插入过程相反,所删除的是处于顶堆的节点。比如我们删除最小堆的堆定点1。
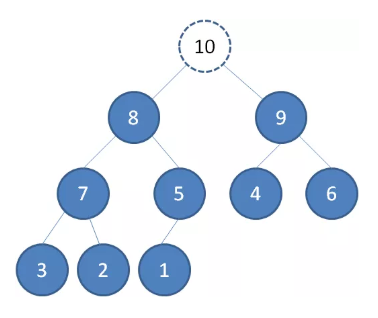
这时候,为了维持完全二叉树的结构,我们把堆的最后一个节点10补到原本堆顶的位置。
接下来我们让移动到堆顶的节点10和它的左右孩子进行比较,如果左右孩子中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”。
继续让节点10和它的左右孩子比较,左右孩子中最小的是节点7,由于10大于7,让节点10继续“下沉”。
这样一来,堆重新得到了调整。
从上面的分析可知,显然不管是插入还是删除操作,堆的自我调整都与深度成正比,故时间复杂度为
$O(logn)$
6.堆排序
6.1 构建二叉堆
构建二叉堆,也就是一个把一个无序的完全二叉树调整为二叉堆,本质上就是让非叶子节点依次下沉。
我们举一个无序完全二叉树的例子
首先,我们从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左右孩子中最小的一个,则节点10下沉。
接下来轮到节点3,如果节点3大于它左右孩子中最小的一个,则节点3下沉。
接下来轮到节点1,如果节点1大于它左右孩子中最小的一个,则节点1下沉。事实上节点1小于它的左右孩子,所以不用改变。
接下来轮到节点7,如果节点7大于它左右孩子中最小的一个,则节点7下沉。
节点7继续比较,继续下沉。
至此一个无序的完全二叉树成为了最小堆。
6.2堆排序过程
堆排序是利用堆的自我调整实现的。
例如给定一个数组,对数组进行排序,使数组元素从小到大排列。
首先,我们要根据给定的数组构建一个最大堆。当我们删除一个最大堆的堆顶(并不是完全删除,而是替换到最后面),经过自我调节,第二大的元素就会被交换上来,成为最大堆的新堆顶。
6.3算法步骤
- 根据无序数组构建二叉堆
- 循环删除堆顶元素,移到数组尾部,调节产生新的堆顶
6.4 堆排序的复杂度
空间复杂度
因为没有开辟额外的集合空间,所以复杂度是O(1)
时间复杂度
堆排序所需要的时间主要有两部分组成,一是构造二叉堆的时间,二是循环的时间
第一步无序数组构成二叉堆,需要进行$n/2$ 次循环。第一步计算规模是$(n/2)*logn$
时间复杂度$O(nlogn)$
第二步,需要进行$n-1$次循环。每次循环调用一次
7 优先队列
7.1 优先队列种类
优先队列不在遵循队列先入先出的原则。
- 最大优先队列,无论入队顺序,当前最大的元素优先出队
- 最小优先队列,无论入队顺序,当前最小的元素优先出队
比如有一个最大优先队列,它的最大元素时8,那么虽然元素8不是队首元素,但出队的时候仍然让8出队
7.2 利用堆的特性实现优先队列
堆的特性:
- 最大堆的堆顶是整个堆中的最大元素
- 最小堆的堆顶是整个堆中的最小元素
因此,可以用最大堆来实现最大优先队列,最小堆实现最小优先队列。
7.2.1入队操作
插入新节点5
新节点5上浮到合适位置
7.2.2 出队操作
把原堆顶节点10 “出队”
最后一个节点1替换到堆顶位置
节点1下沉,节点9成为新堆顶
7.3 优先队列的时间复杂度
因为二叉堆节点上浮和下沉的时间复杂度都是$O(logn)$ , 所以优先队列入队和出队的时间复杂度也是$O(logn)$